技術資料　配管内を流れる液体の流量と圧力の関係

流量と圧力の関係　（液体の場合）

配管内を流れる流体の流量と流速の関係は

Ｑ＝Ｃ×Ａ×Ｖ　　　で表せます。

ここで、Ｑ：流量　　Ｃ：流出係数　　Ａ：流路面積　　Ｖ：流速

V=（2×Ｐ÷ρ）^0.5     ベルヌーイの定理の応用より

Pv = 1/2 × ρ ×  V ^2　               Pv ：動圧

Ｑ＝Ｃ×Ａ×（2×Ｐ÷ρ）^0.5　　　　　Ｑ：流量 m^3/sec       Ｐ：圧力　差圧（パスカル）　　　ρ（ロー）：流体密度 kg/m^3

Ｐ＝（Ｑ÷（C×A））^2×（ρ÷2）

液体の場合を考えてみると

内径150mmの水平配管に、100m³/h の流量で水が流れていて、その時の配管内の圧力が 100kPa(G)とし、配管下流にバルブが設置されていてバルブの２次側が大気開放されているとします。配管内の圧力が 200kPa(G) に上昇した場合の流量はいくらになるか？

配管の下流側の負荷（抵抗）は変わらず、配管２次側のバルブを操作しないとして考え
Ｑ＝Ｃ×Ａ×（2×Ｐ÷ρ）^0.5　式の Ｑ＝100m³/h   Ｐ＝100kPa(G)   ρ＝1000kg/m³
を代入することで求められます。ここで　Ｃ　、　Ａ　　、　2   の項は一定と考え、式から省きます。

流量Ｑは（Ｐ÷ρ）^0.5 に比例します、つまり圧力Ｐの平方根に比例し、密度ρの平方根
に反比例します。

配管下流側の負荷（抵抗）は変わらないとすると、圧力Ｐは配管内の圧力の変化として考えることができるので、上昇した圧力 200kPa(G) と元の圧力 100kPa(G) の比として考えることができます。

つまり、200÷100 = 2    圧力Ｐが２倍になったことになります。

流量Ｑは圧力Ｐの平方根に比例するので、√２　＝　1.4142 になり、流量は 1.4142 倍になります。

水の密度ρは圧力が変わっても変わらないのでρ（ロー）の項は計算は不要となります。

圧力が200kPa(G)に上昇した時は　Ｑ＝Ｃ×Ａ×（2×2÷ρ）^0.5　　となり

流量は 100m³/h  ×  1.4142   ＝　141.42  m³/h  になります。

このときの流速 Ｖ は、V=（2×Ｐ÷ρ）^0.5     ベルヌーイの定理の応用より、圧力が２倍になるので
流速 Ｖ　は √２ = 1.4142 、流速は 1.4142倍になります。

ベルヌーイの定理とはエネルギー保存の法則を流体に当てはめたものですが、上のベルヌーイの定理の応用とは圧力と流速および流体密度の関係式であって、圧力が上がる（ポンプ圧など）と流速が速くなり流量が大きくなる関係式を求めるものであり、圧力のエネルギーが変化した場合です。

この圧力（動圧）：Ｐと流速：Ｖ、流体密度：ρの関係式はベルヌーイの定理より求めています。

（水平配管内を流れる水の圧力変化による流量変化を考え、位置エネルギー及び粘性の影響は無いものとして考えた場合です。）

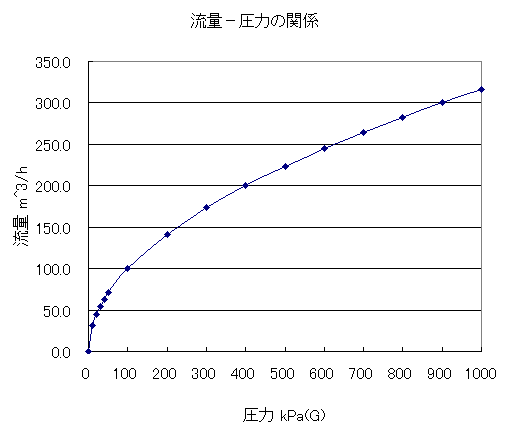
配管内を流れる水の圧力と流量の関係は上のグラフになります。

流量は圧力の平方根に比例し、圧力は流量の２乗に比例します。

流量を２倍に増やすには圧力を４倍にする必要があります。

流量を１／２（半分）にするには圧力を１／４にします。

圧力配管内を流れる水の流量の計算

基本式　　　　　Ｑ＝Ｃ×Ａ×（２×Ｐ÷ρ）^0.5
Ｑ：流量（m³/sec）
Ｃ：流出係数（約0.6～0.8）
Ａ：流路面積（m²）
Ｐ：圧力、差圧　（Ｐａ）
ρ：水の密度(kg/m^3）

例１．
内径100mmの配管内の圧力が0.1MPa(G)として、配管の下流側が大気開放されているとき配管を流れる水の流量はいくらか？

配管の長さによる摩擦抵抗は無視して考えた場合。
流出係数は 0.7 とする。
Ｑ＝Ｃ×Ａ×（２×Ｐ÷ρ）^0.5　　　基本式
＝0.7×0.007854×（2×100000/1000）^0.5
＝0.7×0.007854×14.142
＝0.07775 （m³/sec）
＝279.9　　（m³/h）

内径100mmの配管の内径面積は 0.007854m²、流出係数 0.7  、0.1MPa(G)=100000 Paとして計算

このときの流速は 9.896 m/sec とかなり大きな値である。一般的にはこのような配管の使用方法は少ないだろうが、実際に流すと 100mm の配管出口側はジェット水流のように吐出するだろう。

この流速で配管長さを 10m にした場合には約8600mmAq（84.3kPa）、配管長さを 100m にした場合は約86000mmAq（843kPa）の圧力損失となるために、配管長さを 100m にした場合に、元圧は0.1 MPa(G) ＋ 0.843MPa  ＝　0.943 MPa(G) 以上必要になることになる。

ポンプなどで送る場合にはパワーのあるポンプが必要になることが判る。

上の例は大まかな計算なので、参考程度にみてください、問い合わせには応じられません。

例２．
内径13mmの水道管内の圧力が0.2MPa(G)として、配管の下流側が大気開放されているとき 配管を流れる水の流量はいくらか？　配管の長さによる摩擦抵抗は無視して考えた場合。
流出係数は 0.7 とする。
Ｑ＝Ｃ×Ａ×（２×Ｐ÷ρ）^0.5　　　基本式
＝0.7×0.0001327×（2×200000/1000）^0.5
＝0.7×0.0001327×20
＝0.0018578 （m³/sec）
＝6.688　　　（m³/h）

内径13mmの水道管の内径面積は 0.0001327m²、流出係数 0.7  、0.2MPa(G)=200000 Paとして計算
この例は一般家庭の水道管でどのくらいの水量が出るのか？　計算してみたが、一般家庭の蛇口を全開にしても 6.688 m³/h は流れないと考えられる。

これは蛇口を全開にしても 13mm の内径相当の開口面積はないと推測でき、蛇口（バルブ）は栓構造をしていて、グローブバルブ（ノンフルボア）に近い構造のために 100％　開口に相当しない。

また一般家庭の水道管の元圧も一定でなく、立地条件による高低差、家庭ごとの配管設置条件による圧力損失によって蛇口を全開にしたときの圧力は 0.1 ～ 0.2 MPa(G) 程度ではないだろか？

水道本管の元圧は 0.3 ～ 0.5 MPa(G) 程度ありそうだが。

一般家庭の蛇口を全開にしたときの水量は、おおよそ 3 m³/h 程度なのではないだろうか？

Ｑ＝0.7×0.000063617×（2×200000/1000）^0.5
＝0.7×0.000063617×20
＝0.00089064 （m³/sec）
＝3.2      　　　（m³/h)

圧力が 0.2 MPa(G) とした場合は、蛇口全開の開口面積は 約 9mm に相当する水量になる。

内径 9mm の開口面積 0.000063617 m²

この時の流速は 6.7 m/sec になり配管長さを 10m にした場合には約 345kPaの圧力損失となるため
元圧は 0.2 MPa(G) ＋ 0.345MPa  ＝ 0.545 MPa(G) 以上必要になることになる。

水道本管の元圧が 0.5 MPa(G)　あったとしても、配管長さが 10m あると、圧力損失が 0.345MPaあるので、0.5 - 0.345 = 0.155 MPa(G) の圧力しか加わらないので、蛇口を全開にしても、2.82 m³/h の流量しか流れない。これが、配管の長さによる圧力損失を加味して計算した場合である。

家庭の水道管 13mm の場合に、蛇口を全開にした場合に 2.8 ～ 3.2 m³/h　の流量は妥当なところではないだろうか。

なお、一般家庭の水道管の口径は 25mm  20mm  13mm  があり、基本料金、メータが異なる
ようなので、試しに計算する場合は自宅の水道管の口径（サイズ）をご確認ください。

配管の摩擦圧力損失については、Darcy weisbach  ダルシー・ワイスバッハの式で求められます。

配管の摩擦圧力損失は配管の長さに比例し、流速の２乗に比例します。配管の長さが２倍になると圧力損失も２倍に、流速が２倍になると圧力損失は４倍になります。

（上の例は大まかな計算なので、参考程度にみてください、問い合わせには応じられません。）

上に掲載した資料は弊社流量計の性能に影響する内容ではありませんので全ての項目について問い合わせには応じられません。